chap2-软件无线电理论基础

软件无线电理论基础

信号采样基本理论

Nyquist采样定理

Nyquist采样定理：设一个频率带限信号$x(t)$，其频带限制在$(0, f_H)$内，如果以不小于$f_s=2f_H$的采样速率对$x(t)$进行等间隔采样，得到时间离散的采样信号$x(n)=x(nT_s)$（其中$T_s=1/f_s$称为采样间隔），则原信号$x(t)$将被所得到的采样值$x(n)$完全地确定。

带通采样定理

带通采样定理：设一个频率带限信号$x(t)$，其频带限制在$(f_L, f_H)$内，如果其采样速率$f_s$满足式：

$$f_s = \frac{2(f_L+f_H)}{(2n+1)}$$

式中，$n$取能满足$f_s≥2(f_H-f_L)$的最大整数$(0,1,2,…)$，则用$f_s$进行等间隔采样所得到的信号采样值$x(nT_s)$能准确地确定原信号$x(t)$。

$(1)$式用带通信号的中心频率$f_0$和频带宽度B也可用式$(2)$表示：

$$f_0 = \frac{2n+1}{4}·f_s$$

式中，$f_0 = \frac{f_L+f_H}{2}$，$n$取能满足$f_s ≥ 2B$（$B$为频带宽度）的最大正整数。

软件无线电中的信号采样

允许过渡带混叠时的采样定理

我们已经知道，无论是Nyquist低通采样还是带通采样所需的采样速率$f_S$都必须大于处理带宽$B$的$2$倍，即满足：

$$f_s ≥ 2B$$

在之前的讨论中，ADC采样前的抗混叠滤波器都假定是理想滤波器，如图$(a)$所示，而实际中通常采样图$(b)$所示的矩形系数为$r,(r = \frac{B_r}{B})$梯形滤波器，$B_r$是由于滤波器不理想所造成的滤波器实际带宽。

如果不考虑滤波器过渡带中的信号是可以混叠的，则采样速率必须取$f_s ≥ 2Br$。

我们不希望由于滤波器的非理想而导致采样速度增加，因此必须想办法削弱滤波器非理想的影响。

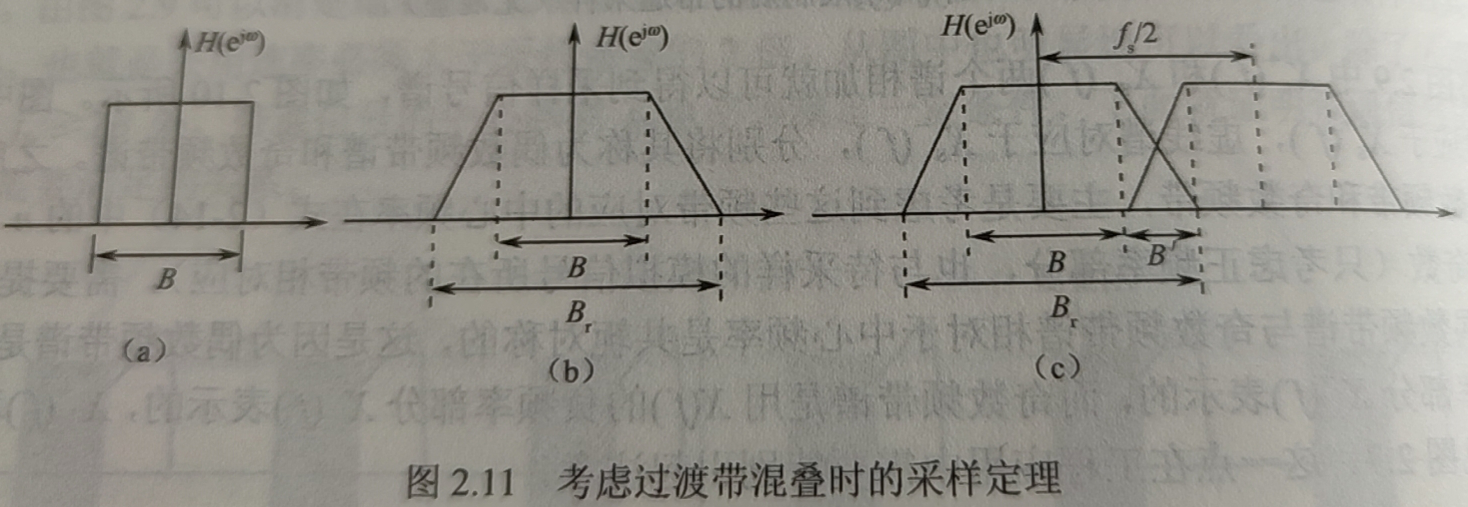
允许过渡带混叠时的采样定理：任何一个中心频率为$f_0$，带宽为$B$的某一带通信号$x(t)$，如果同时满足以下条件：

$$f_0 = \frac{2n+1}{4}f_s\ ,\ f_s≥(r+1)B$$

软件无线电中的正交低通采样

软件无线电所覆盖的频率范围比较宽：$0.1MHz$~$3GHz$，直接采样Nyquist低通采样需要至少$6GHz$。

参考资料

1. 《软件无线电原理与应用》（第2版）第二章